Optimierung in der Produktion

Warum Optimierung?

Optimierungsmethoden spielen in der Produktion eine entscheidende Rolle, da sie dazu beitragen, Ressourcen effizient zu nutzen, Kosten zu minimieren und die Produktionsleistung zu maximieren.

Diese Methoden können eine Vielzahl von positiven Effekten auf die Produktion haben:

Effizienzsteigerung: Durch die Optimierung von Produktionsprozessen können Unternehmen ihre Ressourcen besser nutzen, was zu einer Steigerung der Effizienz führt. Das bedeutet, dass weniger Zeit, Material und/oder Energie benötigt werden, um die gleiche oder sogar eine höhere Menge an Produkten herzustellen.
Kostenreduktion: Optimierungsmethoden ermöglichen es, Kosten zu minimieren, indem sie den Einsatz von Ressourcen optimieren. Dies kann die Herstellungskosten senken und die Wettbewerbsfähigkeit auf dem Markt stärken.
Zeitmanagement: Effektive Optimierung verkürzt die Durchlaufzeiten in der Produktion. Kürzere Produktionszyklen bedeuten, dass Produkte schneller verkauft werden können. Das wiederum verbessert die Kundenbindung und die Fähigkeit, auf sich ändernde Marktanforderungen zu reagieren.
Ressourcennutzung: Optimierung ermöglicht eine bessere Nutzung von Ressourcen wie zum Beispiel Arbeitskräfte, Maschinen und Materialien. Das trägt nicht nur zur Kostenreduktion bei, sondern auch zur nachhaltigen Nutzung von Ressourcen, was in der heutigen umweltbewussten Welt von großer Bedeutung ist.
Qualitätsverbesserung: Durch die systematische Optimierung von Produktionsprozessen können Qualitätsstandards besser eingehalten werden. Dies führt zu weniger Ausschuss, geringeren Nacharbeitskosten und letztendlich zu zufriedeneren Kunden.
Flexibilität und Anpassungsfähigkeit: Optimierungsmethoden tragen dazu bei, Produktionsprozesse flexibler und anpassungsfähiger zu gestalten. Dies ist besonders wichtig in Zeiten sich schnell ändernder Marktbedingungen oder bei der Einführung neuer Produkte.

Zur Veranschaulichung möchten wir anhand eines kleinen Beispiels zum Thema Maschinenbelegung Optimierungsstrategien in der Produktion aufzeigen.

Maschinenbelegung – Welcher Auftrag läuft wann auf welcher Maschine?

Eine wichtige Aufgabenstellung in der Produktion ist die Einplanung von Aufträgen auf Maschinen, die wir im Folgenden anhand eines Beispiels aus der Literatur skizzieren wollen. Die Zahlen und Grafiken sind dem Lehrbuch „Grundlagen des Operations Research” entnommen, adaptiert und gekürzt (s.259 ff)

In diesem Szenario gibt es vier Aufträge (A1 – A4) zu erledigen, die jeweils nacheinander auf zwei Maschinen (M1, M2) laufen. (vgl. Diagramme). Das bedeutet, dass ein Auftrag zuerst auf Maschine M1 gelaufen sein muss, bevor er auf Maschine M2 bearbeitet werden kann.

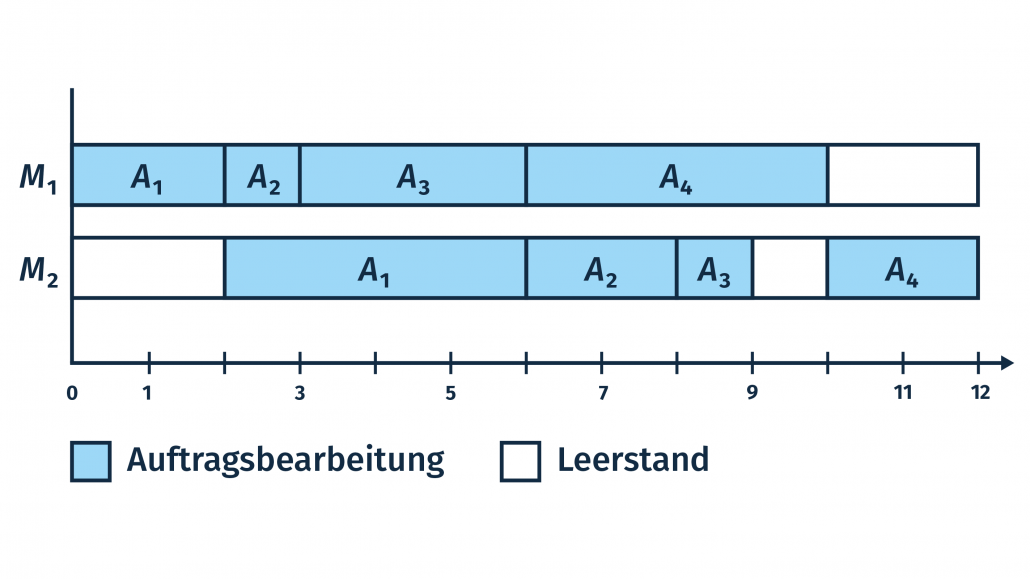
Wenn die Aufträge strikt der Reihe nach erledigt werden, ergibt sich folgender Ablauf:

Das Bild zeigt ein Diagramm mit Maschinen auf der Y-Achse und Tagen auf der X-Achse. Die Aufträge eins bis vier werden in aufsteigender Reihenfolge nach ihrer Auftragsnummer erst auf Maschine 1 und dann auf Maschine 2 eingeplant.

Ist das optimal geplant? Das kommt ganz darauf an, welches Zielkriterium man hat. Wie essenziell diese Angabe für die Optimierung ist, verdeutlichen diese drei Beispiele.

Beispiel 1: Kurze Wartezeiten vor Maschine 2

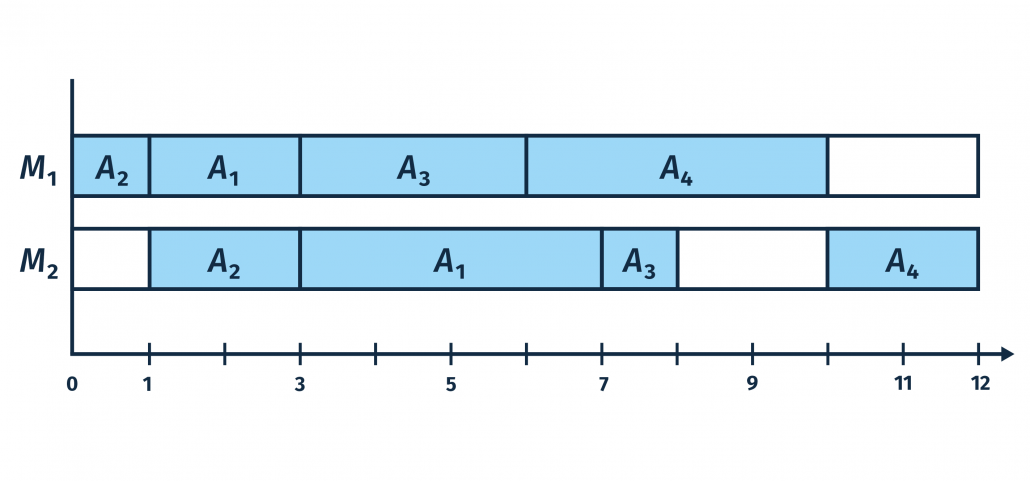
Die Maschine 2 ist direkt abhängig von Maschine 1. Damit sie also möglichst schnell genutzt werden kann, sollte die kürzeste Operationszeit von Maschine 1 als erstes bearbeitet und die weiteren Aufträge aufsteigend nach ihrer Produktionsdauer eingeplant werden.

Damit sieht die Belegung folgendermaßen aus:

Das Beispiel 1 zeigt ein Diagramm mit Maschinen auf der Y-Achse und Tagen auf der X-Achse. Die Aufträge werden in aufsteigender Reihenfolge nach Produktionsdauer auf Maschine 1 eingeplant und danach auf Maschine 2 in gleicher Reihenfolge abgearbeitet.

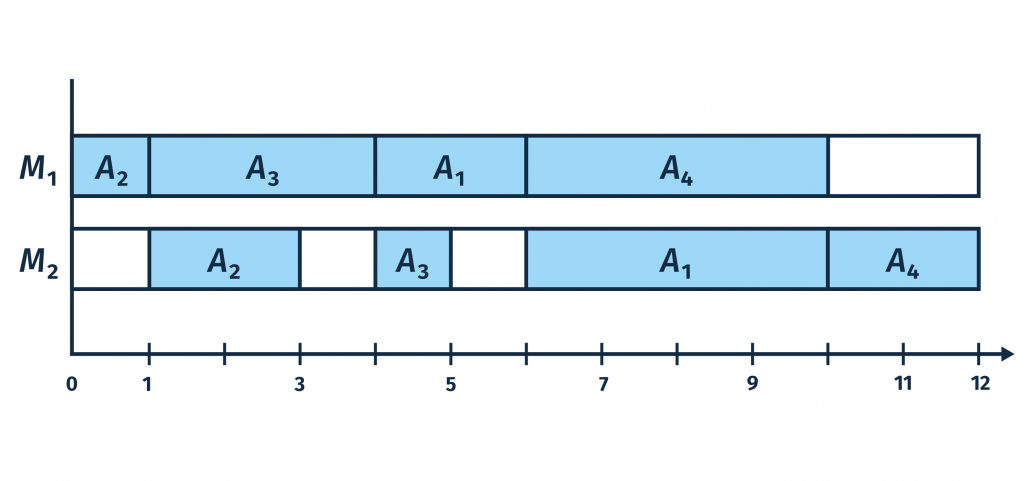
Beispiel 2: Aufträge schnellstmöglich abschließen

Ein anderes Kriterium könnte sein, Aufträge möglichst zeitnah abzuschließen. Dann würden diese direkt hintereinander an den beiden Maschinen eingeplant, ohne Rücksicht auf die Gesamtzeit.

Das Beispiel 3 zeigt eine Tabelle mit Maschinen auf der Y-Achse und Tagen auf der X-Achse. Die Aufträge sind so angeordnet, dass sich in Summe die kürzeste Produktionszeit ergibt.

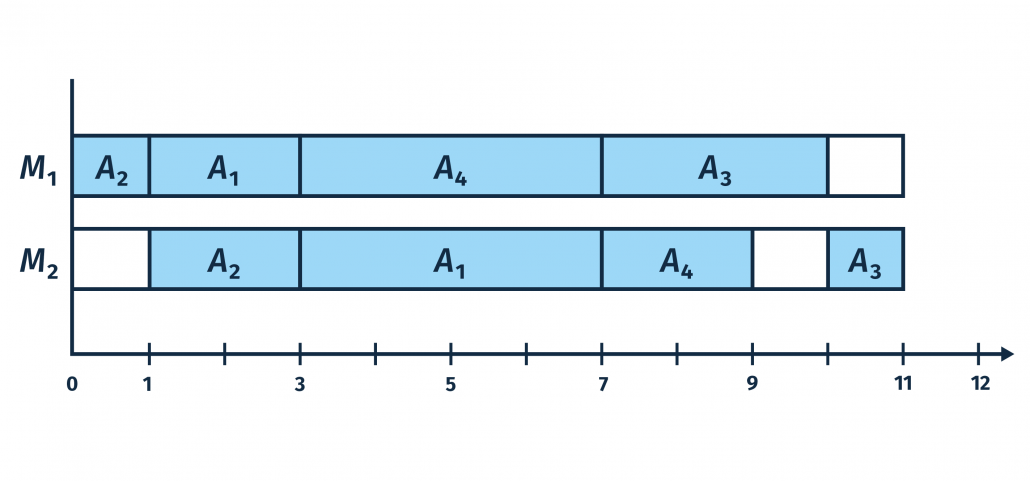
Beispiel 3: Kürzeste Gesamtbearbeitungszeit

Wenn die Maschine 1 die vier Aufträge ohne Unterbrechungen und in der richtigen Reihenfolge produziert, sind für die gesamte Produktionszeit minimal 11 Zeiteinheiten erforderlich. Zehn Zeiteinheiten beansprucht die erste Maschine für die Abarbeitung der Aufträge, und eine weitere Zeiteinheit wird für die Produktion des dritten Auftrages auf Maschine 2 benötigt. Die zweite Maschine hat eine reine Bearbeitungsdauer von 9 Zeiteinheiten, jedoch kann sie zusätzlich zu dem späteren Stillstand von einer Zeiteinheit erst nach der Fertigstellung des zweiten Auftrages auf Maschine 1 beginnen. Somit ist die Dauer von 11 Zeiteinheiten eine untere Schranke für diese Aufgabenstellung. Oftmals kann diese theoretische Schranke jedoch nicht erreicht werden, aber in diesem Fall ist es möglich.

Das Beispiel 2 zeigt ein Diagramm mit Maschinen auf der Y-Achse und Tagen auf der X-Achse. Die Aufträge werden zu erst auf Maschine 1 eingeplant und direkt anschließend daran auf Maschine 1 produziert, so dass die gesamte benötigte Produktionszeit für jeden Auftrag mögichst kurz ist.

Wie man schon anhand dieses kleinen Szenarios sieht, gibt es diverse optimale Lösungen für ein Produktionsproblem. Welche die richtige ist, hängt sehr stark von den aufgestellten Zielkriterien und Rahmenbedingungen ab. Neben der reinen Berechnung der optimalen Lösung ist das Verständnis dieser Randbedingungen ein großer Teil eines Optimierungsprojekts.

Typische Ziele in unseren Kundenprojekten sind die Sicherstellung der Liefertreue sowie die Minimierung der Rüst- und Durchlaufzeiten. Als Randbedingungen wiederum spielen häufig die Maschinenfähigkeiten und Qualifikationen, die Maschinen- und Personalkapazitäten und die Priorisierung innerhalb von Maschinengruppen eine wichtige Rolle.

Lassen Sie uns gemeinsam auch Ihr Problem verstehen und optimieren.